Exploration of the Jerk Limit for Back Protectors

Fred Pieri, V1.1 / 15/11/2024
Edit: 18/11/2024 , typo Edit: 02/12/2025 , adding more drops sample to download

This document is a reflexion to improve the paraglider back protector, it mainly explores the possible implementation of the jerk criterion .

Context

- Based on Zsolt Ero's article published on 02/10/2024: The Future of Paragliding Harness

- As a work for the WG6 group, regarding the current revision of the EN-1651 (Paragliding harnesses requirements)

- The EN-1651 standard is based on the assumption that the role of the protection is to prevent spine compression damage, during a rescue landing.

Goals

The following goals should be kept in mind during the analysis:

• Providing significant value to pilots (safety, ease of use, accessibility, and durability).
• Guaranting to pilots an acceptable level of safety
• Ensuring high repeatability and reproducibility
• Not hindering innovations in design

Selection of the Input Signal

Instantaneous value

Raw Signal Analysis

Measuring jerk directly from raw acceleration data poses challenges because differentiating the acceleration amplifies noise, making the jerk measurement unreliable. Even minor noise fluctuations in acceleration can become exaggerated in the jerk calculation, resulting in a "noisy" jerk signal that fails to accurately represent actual changes.

Consider a theoretical example where the signal is constructed with the following characteristics:

• A baseline at 2 Hz with an amplitude of 1
• Regular noise at 50 Hz with an amplitude of 0.2
• Random noise with an amplitude of 0.1

The jerk is calculated as the slope of the acceleration curve at a specific point:

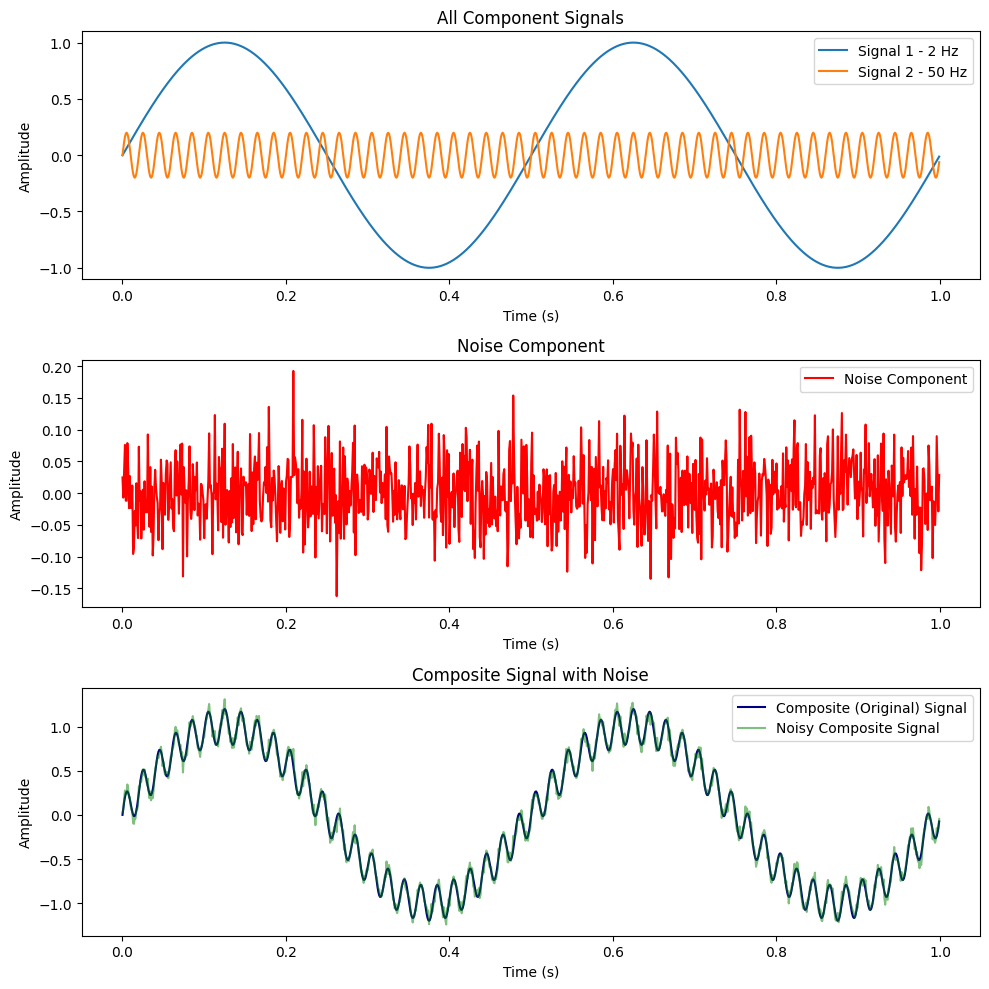
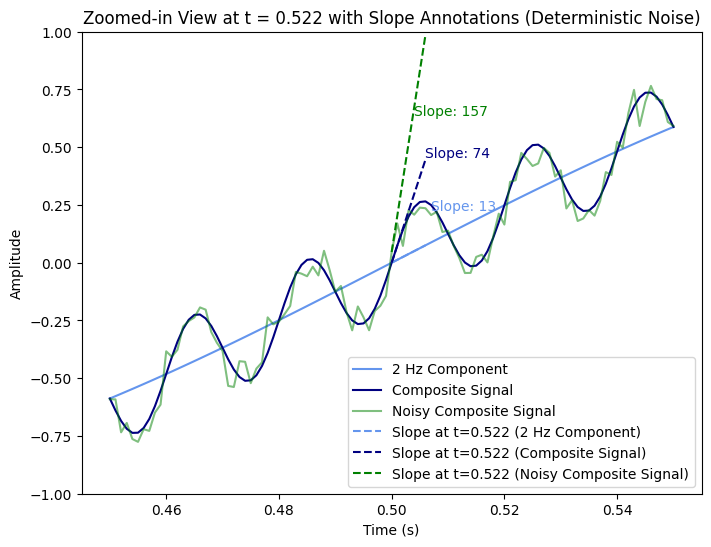
It is evident that the core signal at 2 Hz has a jerk value of 13, while the other signals exhibit significantly higher jerk values (74 for the combined signal and 157 for the combined signal with added noise).

Here is the signal and its derivative:

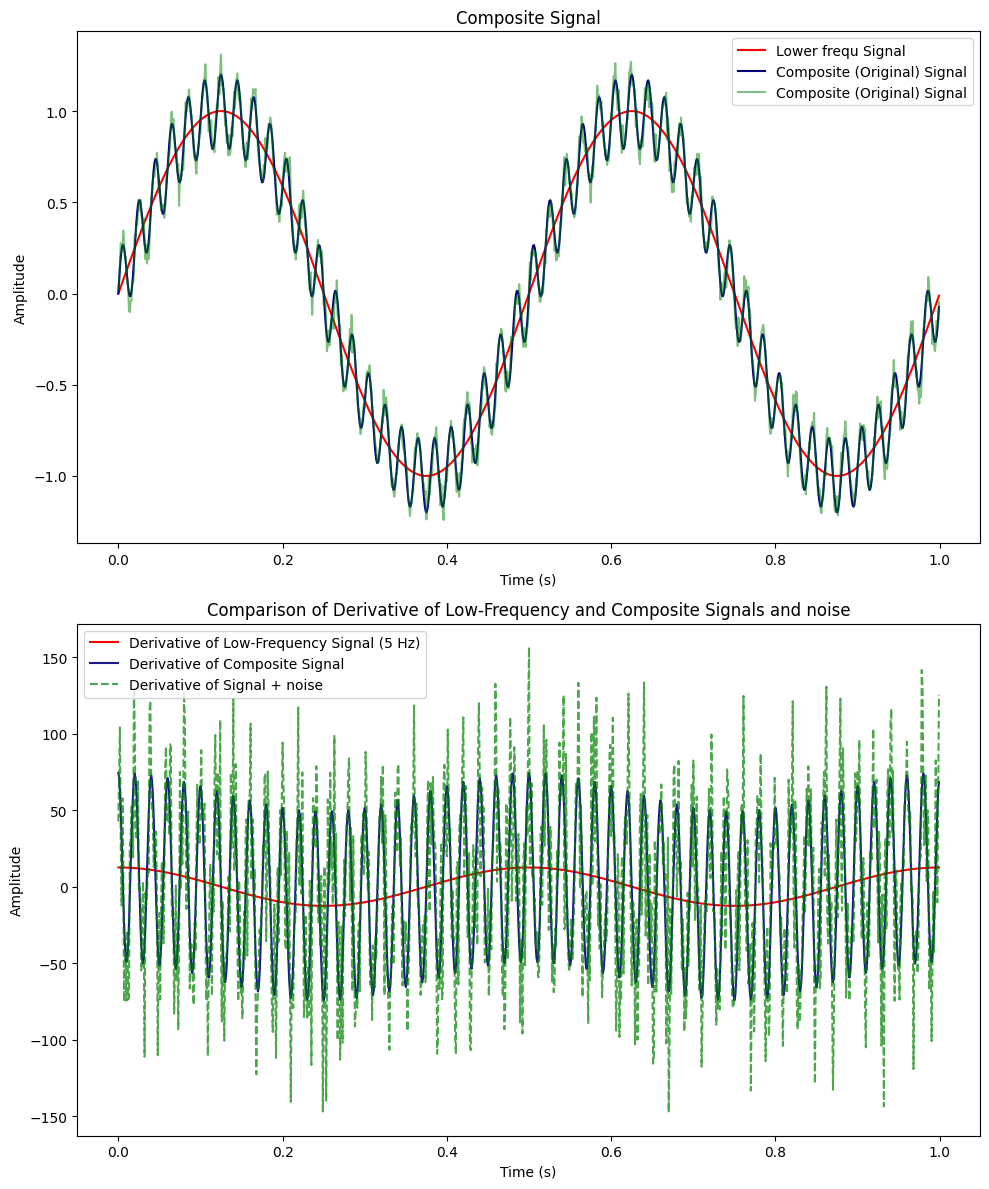
Maximum Values of Signal Derivatives:

• Low-Frequency Signal Derivative: 12.6
• Composite Signal Derivative: 74.4
• Noisy Composite Signal Derivative: 156.7

For an instantaneous jerk of 12.6 for the base signal, the value increases to 157 when accounting for the added noise.

Assessing Real Noise During a Drop

Below is the data from a drop test of a HALO harness prototype, measured at the Ozone Office:

Click for live graph , below zoom on the first impact

Although the noise is less significant than in our theoretical example, let’s examine what this means in terms of repeatability on several drops on several harnesses.

Protocol:

• All tests were conducted on the same day at the Ozone Office
• Approximately 4 minutes elapsed between each drop
• Within the same model series of drops, the harnesses were kept in position on the dummy

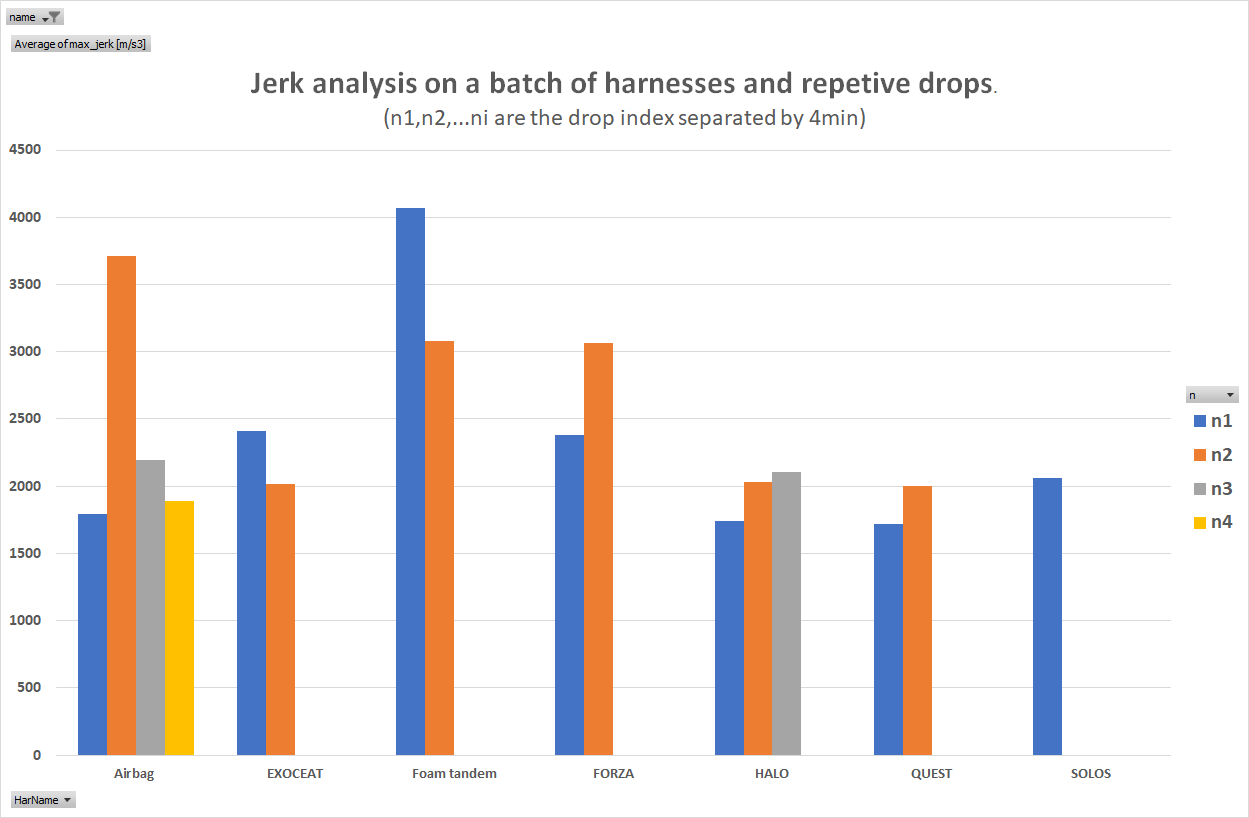
Clearly, the repeatability is not sufficient.

To address this issue, we can consider several approaches:

• Applying a low-pass filter to the acceleration data before calculating the jerk
• Using a rolling average for the acceleration or the jerk
• Defining a range and measuring the jerk between two points:
  • Using a time-based criterion: "maximum jerk found within a time window of X milliseconds"
  • Using an acceleration-based criterion: "maximum jerk found between 5g and 15g, or 20% to 80% of the maximum peak"

Alternative Approaches

Rolling average/Filter Approaches

Rolling Average on the Jerk

We can immediately set this idea aside, as the derivative introduces large spikes or can even approach infinity at points of rapid change due to noise. This significantly distorts the average and leads to misleading results.

Rolling Average on the Acceleration

While mathematically more accurate, the rolling average on acceleration also has its limitations. The effect of a rolling average depends on two factors:

• F: Sampling frequency of the input signal (e.g., 1200 Hz)
• M: Window size (e.g., 2,3, 10, 20 measurements)

Given these parameters, the rolling average can be understood as a low-pass filter with the following response (a 'SINC' curve):

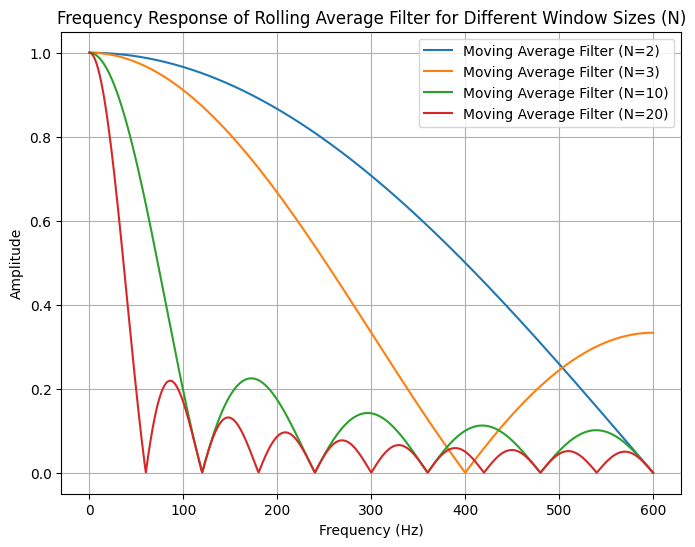
The response of a rolling average is not satisfactory as it requires adjusting its parameter (window size) for different test setups, and it also assumes a constant sampling rate. A better approach would be to use a low-pass filter.

Low-Pass Filter

My expertise in signal filtering is limited, so I rely on a classic Butterworth filter.

The Butterworth filter is preferred over a moving average filter because of its smooth frequency response, sharper roll-off, and flexibility in controlling cutoff frequencies. Unlike the moving average filter, which has an oscillatory response and less effective attenuation, the Butterworth filter provides a predictable, flat passband and can be configured to minimize phase distortion.

Below is the response of a Butterworth filter with a cutoff frequency of 50 Hz for different filter orders:

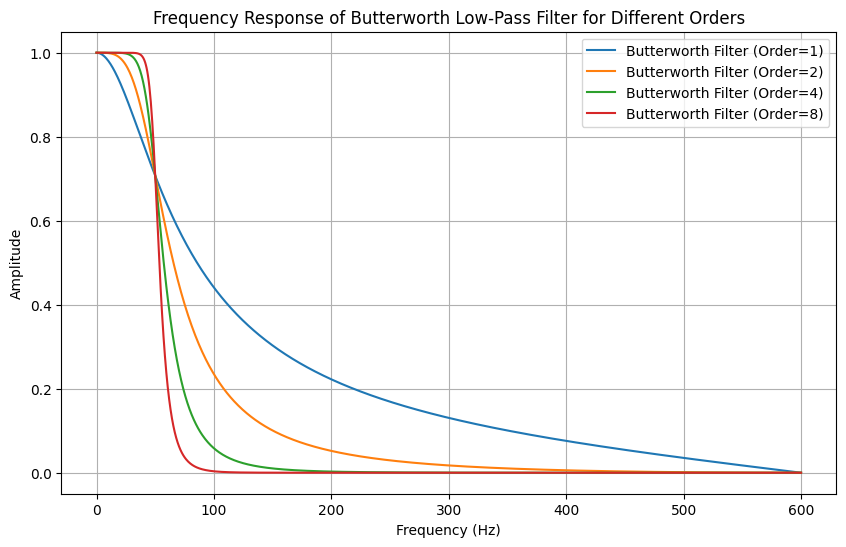
This is the concrete HALO drop data passed through a Butterworth filter with a cutoff frequency of 50 Hz and an order of 8:

Although the noise has been reduced, the filtering has also affected the maximum peak.

Range Approaches

Time Criterion

For example: Measure the jerk over a rolling time window of 0.01 seconds.

Any time criterion should be chosen carefully. If the window is too wide, it will not catch high jerk values, and if it is too narrow, it will be overly influenced by noise. Below is a schematic representation of a window that is too wide:

Acceleration Criterion

This criterion can be absolute or relative to the maximum g peak:

• Absolute: Measure the jerk between 5g and 30g
• Relative: Measure the jerk between 20% and 80% of the maximum g peak

For both scenarios, situations may arise where the criterion is not adequate:

• If the protector only reaches 29.9g but exhibits a huge jerk
• If the protector has a large jerk but a maximum peak of only 15g (e.g., a very thick, thin honeycomb construction protection)

Conclusion

While the Jerk criterion is documented and seems an interesting approach, it opens some questions and challenges :

• The first question that arise is: does the approach of limiting the jerk stand on its own, or is it an improvement that complements the G*duration model?
• It remains to be studied if this sophistication improves real-world paragliding practice
• Technical criteria are still to be refine for a real life implementation.

To go further:

• Examine deeply all the scientific articles, to be sure that all the hypothesis in the previous quoted studies are valid in paraglider crash case.
• Explore the different range criteria possible to define the Jerk criteria.

Side Notes

Theoritical thickness protector

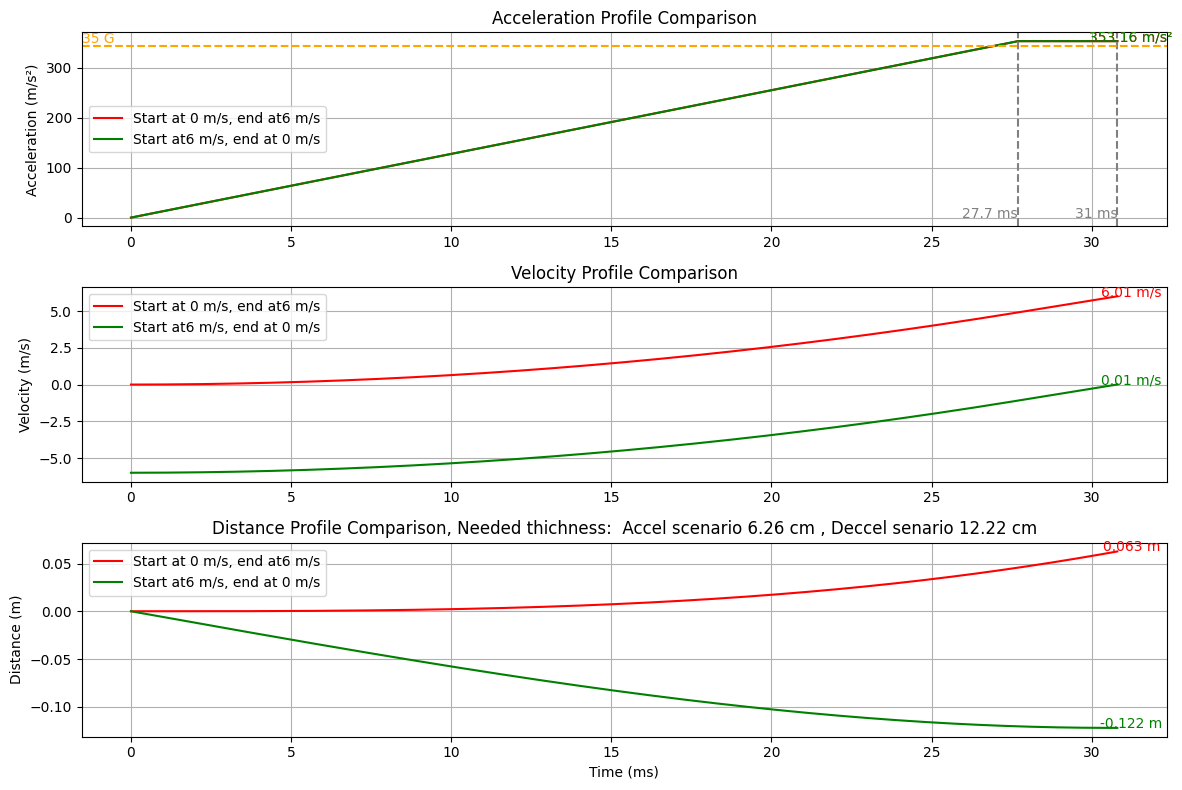
In a previous post by Zsolt, a theoretical minimum thickness of 6.22 cm was calculated based on the following criteria:

• A peak acceleration of 36 G
• Max Jerk of : 1300 g/s
• A time duration exceeding 35 G of 7 ms
• An initial speed of 6 m/s (assumed from the previous context)

Using the same criteria, we recalculated a absolute minimum thickness of 12.2 cm.

Based on Zsolt's assumption of an additional 20% for uncompressed material, the minimun thickness of a protection would be approximately 15 cm. However, it is worth noting that, in practice, foam protectors tend to compress by around 70% so an extra thickness of 30% is more realistic.

Below is a graph showing both scenarios, with the green line representing the scenario that should be considered, starting from acceleration to distance (protection thickness) via integrations. The red line is the incorrect calculation.

Here the Colab (python) document with the code for peer review:

Minimmal Thickness requirement

Absolute measurement criteria (e.g., deformation limited to 10 cm) are not ideal for the following reasons:

• Variability in Inflatable Protections: For inflatable protectors, the deformation depends heavily on internal pressure and altitude. This makes consistent and reliable measurement difficult.
• General Measurement Challenges: Regardless of the type of protection, accurately measuring thickness requires defining a fixed point of reference and a direction. Without the harness in its flight configuration, determining these is ambiguous, leading to inconsistent results across tests and setups.
• Complex Geometries: Protectors often feature curved or non-linear designs to provide ergonomic, safety or aerodynamic advantages. Measuring distance on such shapes is inherently complex, especially when curvature might occur in multiple directions simultaneously.
• Potential Design Exploitation: We strongly advocate for performance result criteria, as arbitrary criteria can be prone to goal subvertions and misinterpretation.
  As an example :It allows designers to focus solely on protecting a small critical area while filling the remaining space with lightweight, ineffective materials to meet shape requirements without enhancing overall safety.

These issues highlight that absolute dimensional criteria may lack the robustness and adaptability needed for a meaningful evaluation of protective systems. Below some cad design that illustrate the different problematic:

The challenge is to give the thickness of these protections:

The cad drawing (format STEP) can be downloaded here:

• Double Curved Model
• Inflated Model
• Torus Model

Egg breaking

See below a acceleration curve during an 'impact' :

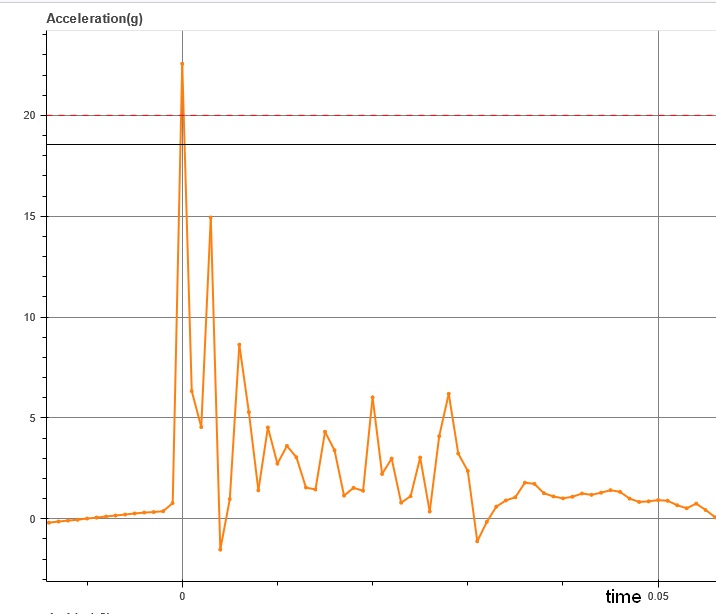
This impact was max peak of 22 g with a jerk around 20 000 g/s

below a video of this 'impact' :

My fingers and my hand were not broken or injured during this experience. :-) This example illustrates that a number of Jerk alone or a number of G alone does not allow conclusions about the danger to humans.

Sources

Rolling average

• https://www.analog.com/media/en/technical-documentation/dsp-book/dsp_book_ch15.pdf

Data sample

Here some real data to download from 3 drops done at the Ozone's lab on the same harness, drop spaced by around 2-4min :

• Data CSV format ( updated 02/12/2025)