
Fred Pieri, V1.1 / 18/11/2024 Edit: 02/12/2025 , adding more drops sample to download
Ce document explore les possible améliorations des protections dorsales des sellettes de parapente et notamment la possible mise en oeuvre du critère de jerk comme critère.
Dans cette version francaise, les graph et certain mot clé ne sont pas traduit. Pour toute ambiguïté, se référer à la version anglaise.- Basé sur l'article de Zsolt Ero publié le 02/10/2024 : L'avenir des Sellettes de Parapente
- En tant que travail pour le groupe WG6, concernant la révision actuelle de l'EN-1651 (Exigences pour les sellettes de parapente)
- La norme EN-1651 repose sur l'hypothèse que le rôle de la protection est de prévenir les dommages par compression de la colonne vertébrale lors d'un atterrissage sous le secours.
Les objectifs suivants doivent être pris en compte lors de l'analyse :

Mesurer directement le jerk à partir des données d'accélération brutes pose des défis car la différenciation (calcul de la derivée) de l'accélération amplifie le bruit, rendant la mesure du jerk peu fiable. Même de légères fluctuations de bruit dans l'accélération peuvent devenir exagérées dans le calcul du jerk, résultant en un signal de jerk "bruyant" qui ne représente pas fidèlement les changements réels.
Considérons un exemple théorique où le signal est construit avec les caractéristiques suivantes :
Le jerk est calculé comme la pente de la courbe d'accélération à un point spécifique :
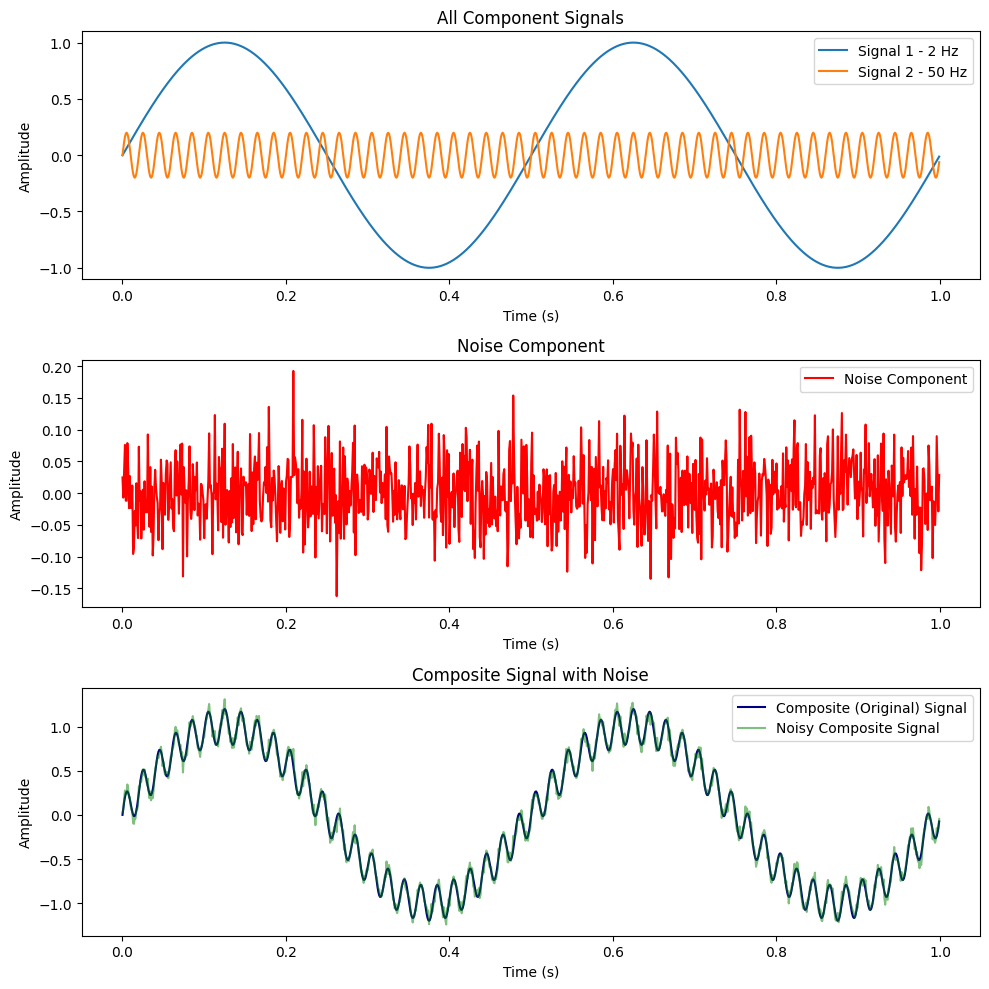
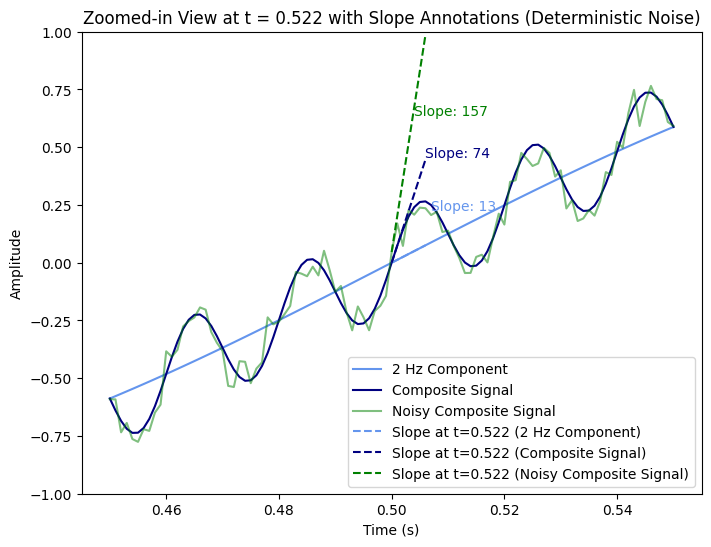
Il est évident que le signal de base à 2 Hz a une valeur de jerk de 13, tandis que les autres signaux présentent des valeurs de jerk significativement plus élevées (74 pour le signal combiné et 157 pour le signal combiné avec bruit ajouté).
Voici le signal et sa dérivée :
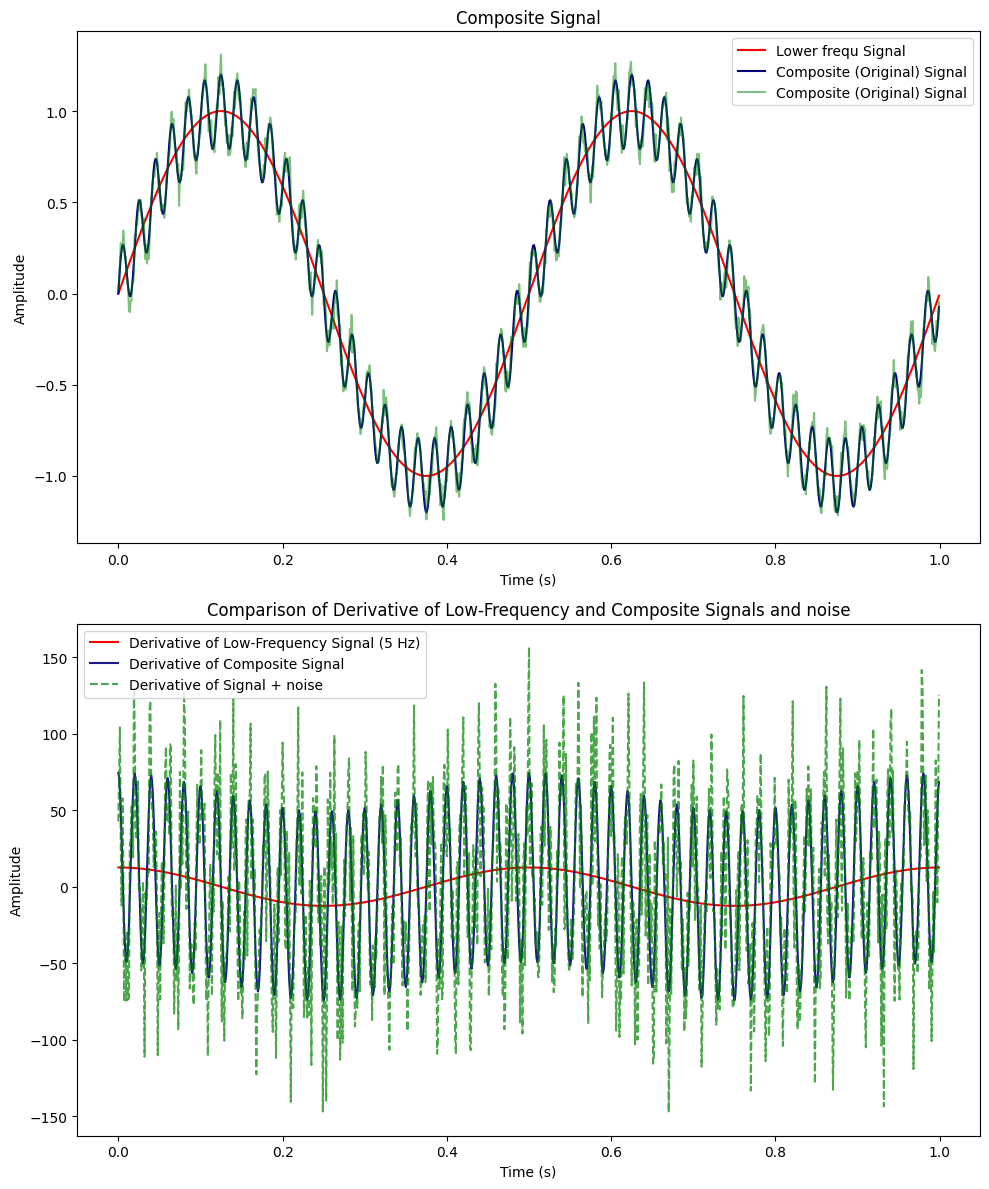
Valeurs Maximales des Dérivées des Signaux :
Pour un jerk instantané de 12.6 pour le signal de base, la valeur augmente à 157 en tenant compte du bruit ajouté.
Voici les données issues d'un test de chute d'un prototype de sellette HALO, mesurées au bureau d'Ozone :
Cliquez pour un graphique interactif, ci-dessous un zoom sur le premier impact
Bien que le bruit soit moins significatif que dans notre exemple théorique, examinons ce que cela signifie en termes de répétabilité sur plusieurs chute sur plusieurs sellettes.
Protocole :
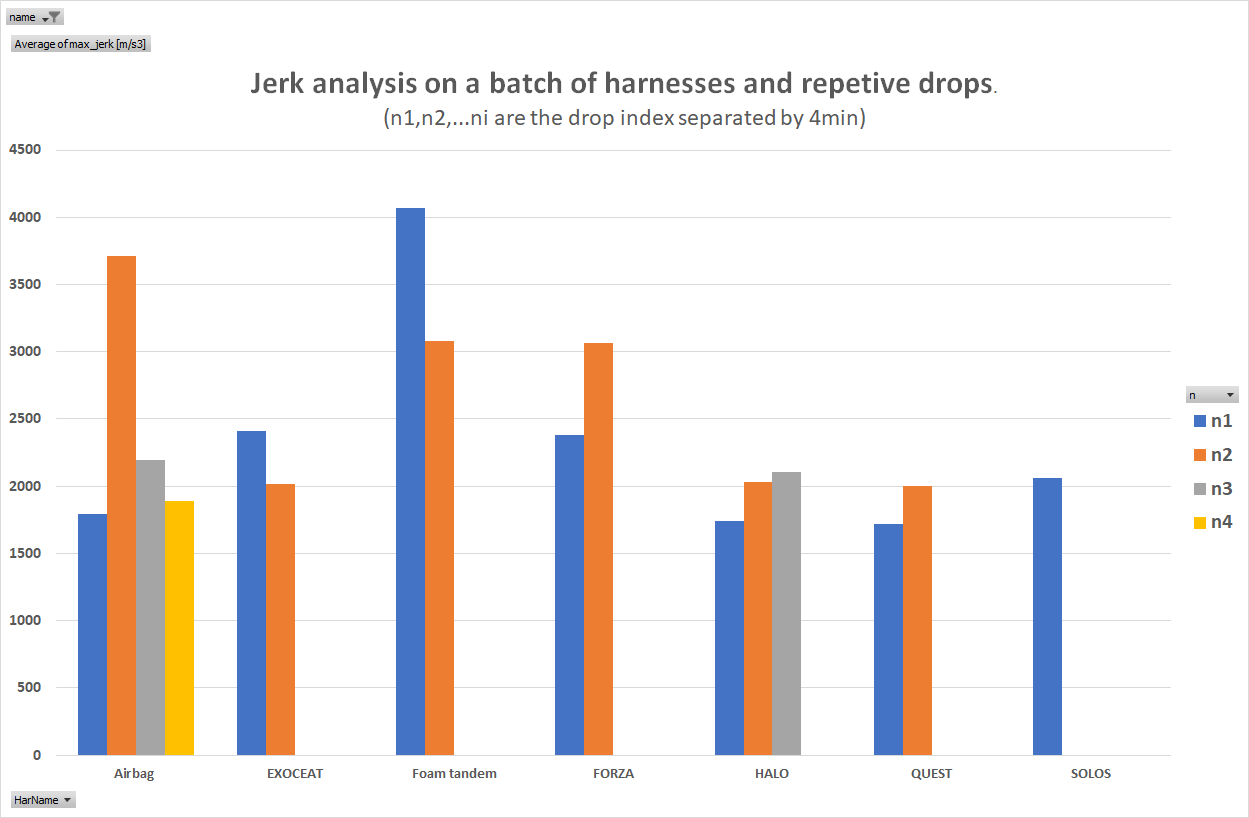
Il est clair que la répétabilité n'est pas suffisante.
Pour résoudre ce problème, plusieurs approches peuvent être envisagées :

Cette idée peut être écartée immédiatement, car la dérivée introduit de grands pics ou peut même approcher l'infini à des points de changement rapide en raison du bruit. Cela déforme considérablement la moyenne et entraîne des résultats trompeurs.
Bien que mathématiquement plus précise, la moyenne glissante sur l'accélération a également ses limites. L'effet d'une moyenne glissante dépend de deux facteurs :
Étant donné ces paramètres, la moyenne glissante peut être vue comme un filtre passe-bas avec la réponse suivante (une courbe 'SINC') :
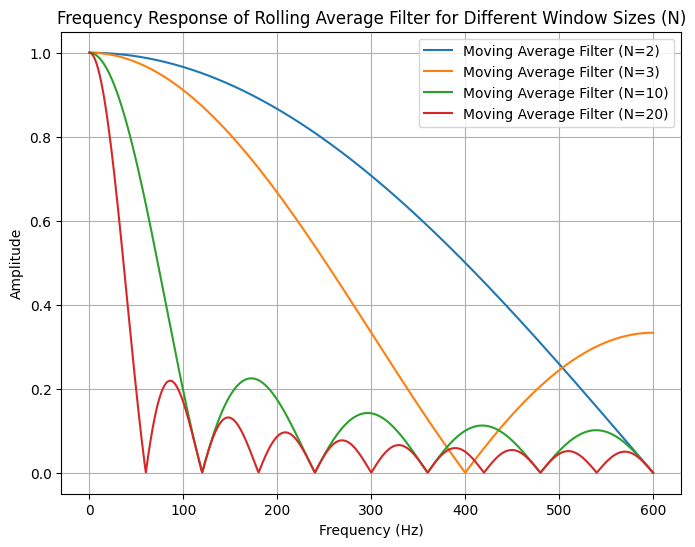
La réponse d'une moyenne glissante n'est pas satisfaisante car elle nécessite un ajustement de son paramètre (taille de la fenêtre) pour différents configurations de test, et elle suppose également un taux d'échantillonnage constant. Une meilleure approche serait d'utiliser un filtre passe-bas.
Mon expertise en filtrage de signal est limitée, je me fie donc à un filtre classique de Butterworth.
Le filtre Butterworth est préféré au filtre moyenne glissante en raison de sa réponse en fréquence lisse, de son atténuation plus marquée et de sa flexibilité pour contrôler les fréquences de coupure. Contrairement au filtre moyenne glissante, qui a une réponse oscillatoire et une atténuation moins efficace, le filtre Butterworth offre une bande passante plate et prévisible, et peut être configuré pour minimiser la distorsion de phase.
Ci-dessous la réponse d'un filtre Butterworth avec une fréquence de coupure de 50 Hz pour différents ordres de filtre :
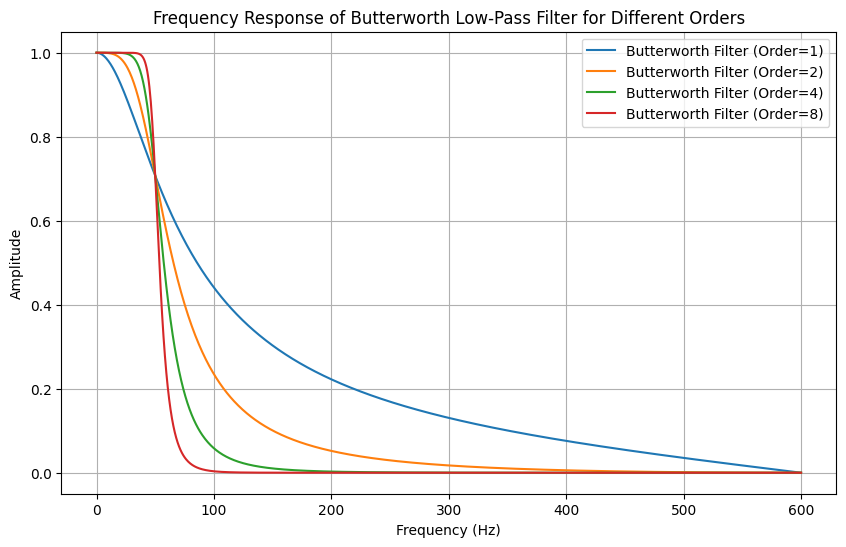
Voici les données concrètes de chute HALO filtrées à l'aide d'un filtre Butterworth avec une fréquence de coupure de 50 Hz et un ordre de 8 :
Bien que le bruit ait été réduit, le filtrage a également affecté le pic maximal.
Par exemple : Mesurer le jerk sur une fenêtre temporelle glissante de 0,01 seconde.
Tout critère temporel doit être choisi avec soin. Si la fenêtre est trop large, elle ne captera pas les valeurs élevées de jerk, et si elle est trop étroite, elle sera trop influencée par le bruit. Ci-dessous une représentation schématique d'une fenêtre trop large :
Ce critère peut être absolu ou relatif au pic maximal en g :
Pour les deux scénarios, il peut y avoir des situations où le critère n'est pas adéquat :

Bien que le critère de jerk soit documenté et semble être une approche intéressante, il soulève certaines questions et défis :

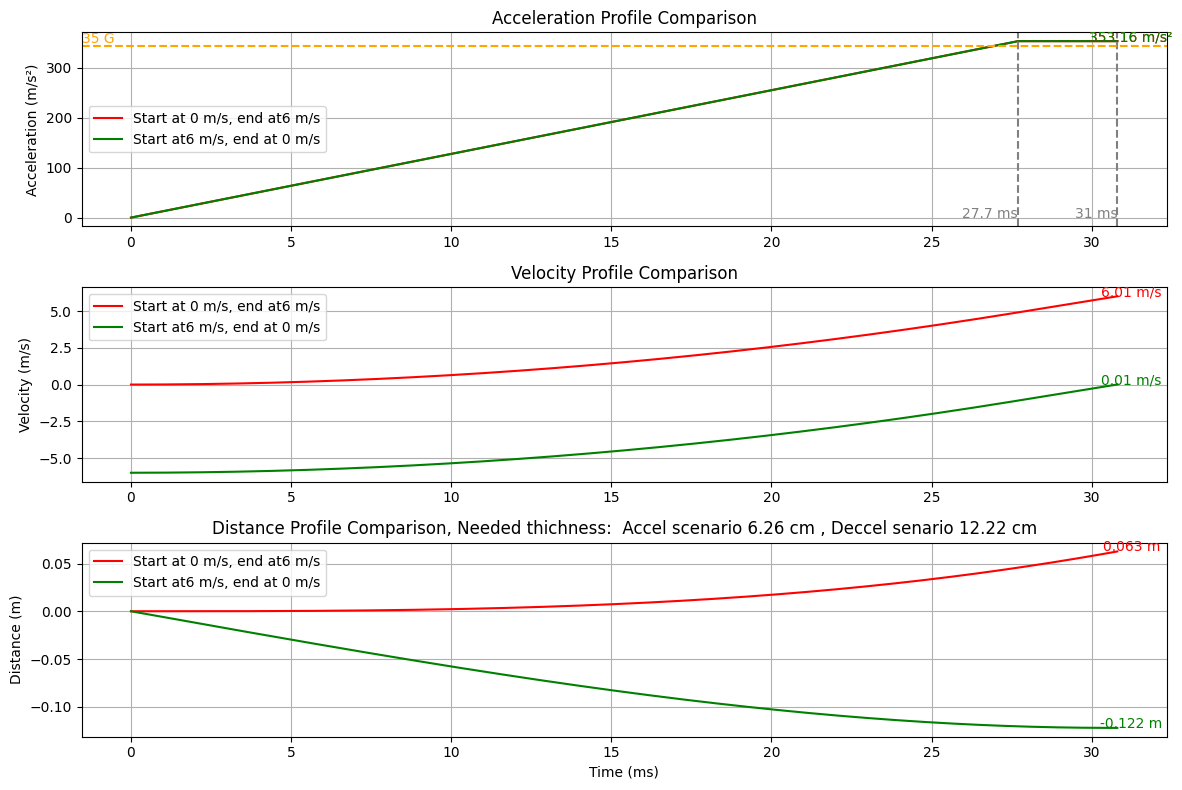
Dans un post précédent de Zsolt, une épaisseur minimale théorique de 6,22 cm a été calculée sur la base des critères suivants :
En utilisant les mêmes critères, nous avons recalculé une épaisseur minimale absolue de 12,2 cm.
En supposant comme Zsolt un supplément de 20 % pour la compressibilité, l'épaisseur totale sera d'environ 15 cm, tout en gardant à l'esprit que d'expérience, les protections en mousse sont plutôt autour de 70 % donc un besoin de 30% et plus realiste.
Ci-dessous se trouve un graphique montrant les deux scénarios, avec la ligne verte représentant le scénario qui doit être
considéré, passant de l'accélération à la distance (épaisseur de protection) via des intégrations. La ligne rouge est le calcul incorrect.
Voici le document Colab (python) avec le code pour revue par les pairs :
https://colab.research.google.com/drive/1iWp5Yp-w_7bZsqWLbQBKYxp_N3ADR-8k?usp=sharing
Les critères de mesure absolue (par exemple, une déformation limitée à 10 cm) ne sont pas idéaux pour les raisons suivantes :
Ces problèmes mettent en évidence que les critères dimensionnels absolus peuvent manquer de robustesse et d'adaptabilité nécessaires pour une évaluation significative des systèmes de protection. Voici quelques conceptions CAD illustrant les différentes problématiques :
Le défi consiste à donner l'épaisseur de ces protections :
Les dessins CAD (format STEP) peuvent être téléchargés ici :

Ci-dessous une courbe d'accélération pendant un "impact" :
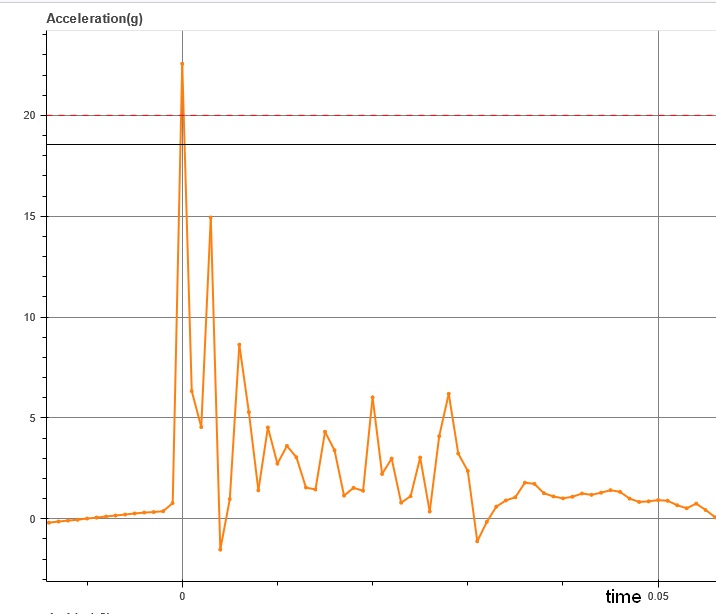
Cet impact a atteint un pic maximal de 22 g avec un jerk d'environ 20 000 g/s
Vidéo de cet "impact" ci-dessous :
Mes doigts et ma main n'ont pas été cassés ou blessés lors de cette expérience !:-) Cet exemple illustre qu'un nombre de jerk seul ou un nombre de G seul ne permettent pas de conclure sur le danger pour les humains.
Voici quelques données réelles à télécharger issues de 3 chutes réalisées dans le laboratoire d'Ozone sur le même sellettes, avec un intervalle de 2-4 minutes entre chaque chute :
Je partage cet ensemble de données car je crois que travailler avec des données réelles est le meilleur
moyen d'apprendre et de progresser. Les données ouvertes et l'examen par les pairs nous aident à grandir
ensemble.
Gardons à l'esprit qu'il ne s'agit que d'un petit échantillon : un sellettes, un laboratoire, un ensemble de
conditions, etc. Tirons des conclusions modestes.